Barber's problem

Tom is a barber in a small town. He owns a little store, several apprentices and good credit for his high quality service. However, as his customers become more and more, he got some problems.
Let's look at the procedure of the haircut at first. Customers are served to change clothes for haircut; after having the hair washed, start the haircut; wash the hair again after that, get the hair dried, change the clothes back and then pay. In Tom's store, he does every haircut, dry work and cash job by himself and leaves the changing clothes and washing hair to his apprentices. Assume each action takes 1 unit time, as shown in Fig. 1.

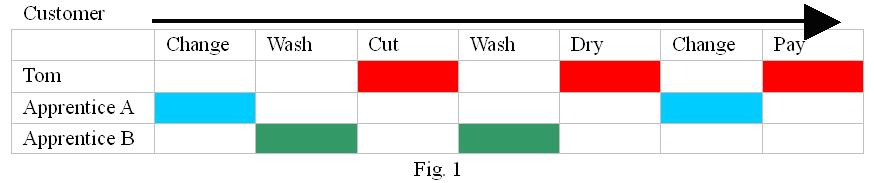
Usually, Tom pipelines the whole procedure, so that he could serve several customers at the same time. Here is the simple case for two customers:

However, when three customers are coming together, the simple pipeline will meet the problem:

At time 5 and time 7, both customer 1 and 3 need Tom. It is too bad, Tom could only do one thing in 1-unit time, but how could he let his customers wait for him with their hair wet?
Of course this is not a big deal for Tom. He just add some wait units in his procedure, as described in Fig. 4:

Nobody will complain for a little rest after haircut and dry, and now all three customers are served in time (Fig. 5).

But what should Tom do for more complicated situations?

Now Tom needs your help. Assuming Tom is able to know when the customer comes, you will judge whether it is possible to add some wait units into the procedure to satisfy:

(1) Enable all the customers to be served as soon as they come (Customers are impatient and will leave if they could not be served in time).
(2) Eliminate the collisions in the pipeline (The collision means that Tom has to serve two and more than two customers at the same time, but many customers can be served to change clothes or wash hair at the same time, because there are enough apprentices)

Some other notes you need to keep in mind:

(1) The wait units you add must be finite.
(2) The wait units can be adjacent.
(3) The procedure for every customer should be the same. Nobody is happy to wait more time than others.
(4) You can only add wait units into procedure, but not exchange or remove any existing step. The original sequence must be kept: Change-Wash-Cut-Wash-Dry-Change-Pay.

There are several test cases in the input.

The following lines describe test cases. Each line for one case is given in such format:

(n₁, n₂, ... n_k ) 0 < n_i <= 20, 0 < k <= 20

It gives the time when customers come. n_i represents the interval time of each sequential customer. The parenthesis means that the customer will come periodically.
For example, assuming the first customer at time 1, if the customers arrive at 1, 3, 5, 7, 9, 11, 13, ... the representation is (2). The representation (1,3,7) represents that the customers will come at time 1, 2, 5, 12, 13, 16, 23, 24, 27, 34...

The example shown in Fig. 5 the description corresponds to the representation (1), and of course more customers will come in time 4, 5, 6, 7...

A line containing "(0)" ends the input.

Your task is to decide whether there is a solution to add FINITE wait units into the haircut procedure to eliminate the collision in the pipeline and enable all the customers to be served as soon as he comes. If it can be solved, print "Yes", otherwise "No", each in one line.

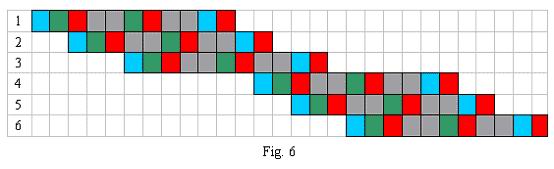
For example, for the input (1), you can add 2 wait units as shown in Fig. 5 above to solve the situation of 3 customers, but when more and more customers come, you can't satisfy everyone except adding more and more wait units. There is not an end. So the answer is "No". For the input (2,3,7), you may add 4 wait units into the procedure to satisfy the pipeline, as explained in Fig. 6. So the answer is "Yes".

(1)
(2,3,7)
(0)

No
Yes

Compiler C C++ Java Python2 Python3

Use advanced editor

Code