Cheat at Math
In Nanjing, a great many students cheat at Mathematics Olympiad contest. Some of them stole the problems. What is worse, some others, like K.W., could even modify the answer sheet to enlarge his scoring. Even though, he is waiting for your help to solve such a complex puzzle, for he cannot solve it himself.
There are four kinds of arcs on the plane: (4 denotes a full circle, 3 denotes ¾ a circle, 2 denotes half a circle, 1 denotes ¼ a circle)
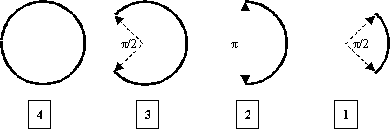
All of the arcs are facing leftwards (as the picture above, one should not rotate them). You are given N <= 1000 arcs on the plane, how many regions are formed out by them (several close regions including the outmost open region)? See the following example:
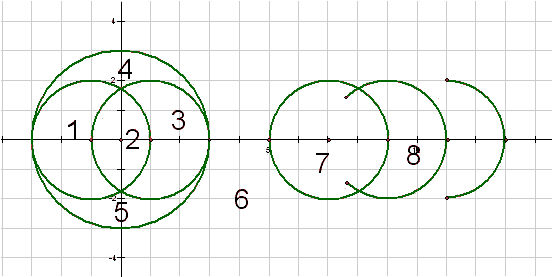
Eight regions are formed out with six arcs.
One non-negative integer N <= 1000 occupies the first line. On each of the 2nd ~ (N + 1)-th line, there will be four integers Xi, Yi, Ri, Ti. An arc of type Ti (1 <= Ti <= 4) with radius of Ri is situated on coordinate (Xi, Yi). We have –5000 <= Xi, Yi <= 5000, 1 <= Ri <= 5000.
A single line denoting the number of regions formed by those arcs.
6 -1 0 2 4 1 0 2 4 0 0 3 4 7 0 2 4 9 0 2 3 11 0 2 2
8
Pay attention to the limit of memory.
Submit
