Black Box

Physicists study atoms hidden in a ``black box". So as to get information on the position of atoms in the box, they cast a laser beam through gates and look at where light gets out from the box. As a computer scientist you are (kindly) requested to interpret the physicists experiments.
Problem
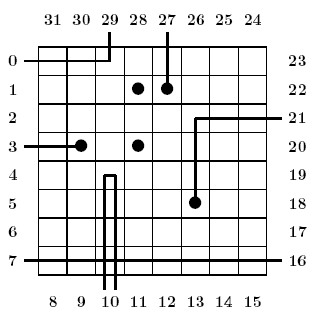
By weighting the box, the physicists already managed to count how many atoms there are (K = 5) . Besides, they adopt a grid model. First, the box is quite simple: this is a flat, N x N box (N = 8) , with 32 = 4 * N gates, which are numbered as shown above. Additionally, following the famous ``no border principle" and a loose application of Pauli exclusion principle, the physicists restrict the available positions to the central 36 = (N - 2)² positions, and they assume that no two atoms occupy the same position. Besides, in the grid model, light is also quite simple:

• Light travels at infinite speed in either of the fourth directions, east, north, west or south. For instance, if the beam enters the box from the west, then it travels eastward.
  
• In the absence of obstacles, light goes straight ahead. See the beam entering at gate 7.
  
• In case it enters a position occupied by an atom, light is absorbed. Then, there is no output gate. See the beam entering at gate 3.
  
• Light is deviated by atoms. Before entering a position whose left (resp. right) neighbor contains an atom, light turns right (resp. left). See the beam entering at gate 0 for an example of a left deviation, and the beam entering at gate 29 for for an example of a right deviation.
  
• Absorption takes precedence over deviation. See the beam entering at position 27.
  
• When a beam is deviated both left and right at the same time, it turns back. See the beam entering at gate 10 and leaving at the same gate 10, because of such a double deviation.
  
• Laws of light combine. See the beam entering at gate 21, which is absorbed after a left deviation.

Input is a log of experiments performed over a given box. The first line is an integer e (0 < e<=32) . Integer e is the number of experiments performed. Then, come e lines, each line being made of two integers. The first integer i is a gate number expressing that the beam enters the box at gate i . The second integer o is either a gate number, expressing that the beam leaves the box at gate o , or the integer `-1', expressing that the beam is absorbed.

If the atom positions can be deduced from the experiments, then your program should output an ascii representation of the box, as N lines of N characters, with atoms being shown as `+' and empty positionsas `-' -- See the first example below. Otherwise, your program should output `NO' on a single line. Notice that `NO' is the correct answer in several situations. More specifically, the experiments may be contradictory (there does not exist a repartition of atoms compatible with the experiments) or non-concluding (there exist several repartitions of atoms compatible with the experiments).

7
0 29
27 -1
21 -1
10 10
3 -1
16 7
6 12

--------
---++---
--------
-+-+----
--------
-----+--
--------
--------

Observe that this output describes the box shown in the introduction.
If input is:
10
0 23
1 28
7 8
20 -1
19 25
10 16
2 31
4 5
12 -1
29 -1
Then, correct output is:
NO