Sylvester construction

A Hadamard matrix of order n is an n x n matrix containing only 1s and -1s, called H_n, such that H_nH_n^T = nI_n where I_n is the n x n identity matrix. An interesting property of Hadamard matrices is that they have the maximum possible determinant of any n x n matrix with elements in the range [-1, 1]. Hadamard matrices have applications in errorcorrecting codes and weighing design problems.

The Sylvester construction is a way to create a Hadamard matrix of size 2n given H_n. H_2n can be constructed as:

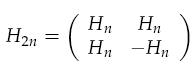
for example:

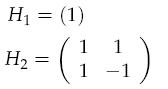
and so on.

In this problem you are required to print a part of a Hadamard matrix constructed in the way described above.

The first number in the input is the number of test cases to follow. For each test case there are five integers: n, x, y, w and h. n will be between 1 and 2⁶² (inclusive) and will be a power of 2. x and y specify the upper left corner of the sub matrix to be printed, w and h specify the width and height respectively. Coordinates are zero based, so 0 ≤ x,y < n. You can assume that the sub matrix will fit entirely inside the whole matrix and that 0 < w,h ≤ 20. There will be no more than 1000 test cases.

For each test case print the sub matrix followed by an empty line.

3
2 0 0 2 2
4 1 1 3 3
268435456 12345 67890 11 12

1 1
1 -1

-1 1 -1
1 -1 -1
-1 -1 1

1 -1 -1 1 1 -1 -1 1 1 -1 -1
-1 -1 1 1 -1 -1 1 1 -1 -1 1
1 1 1 -1 -1 -1 -1 1 1 1 1
-1 1 -1 -1 1 -1 1 1 -1 1 -1
1 -1 -1 -1 -1 1 1 1 1 -1 -1
-1 -1 1 -1 1 1 -1 1 -1 -1 1
-1 -1 -1 -1 -1 -1 -1 1 1 1 1
1 -1 1 -1 1 -1 1 1 -1 1 -1
-1 1 1 -1 -1 1 1 1 1 -1 -1
1 1 -1 -1 1 1 -1 1 -1 -1 1
-1 -1 -1 1 1 1 1 1 1 1 1
1 -1 1 1 -1 1 -1 1 -1 1 -1