Polygon Division

Given a regular polygon, there are numerous ways to divide it into several triangles and/or quadrangles by adding some diagonals that do not properly intersect each other. For example, Figure 4 shows all ten different divisions of a regular pentagon into triangles and quadrangles.

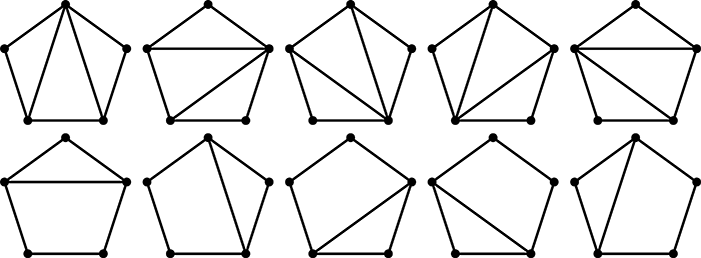
Figure 4: Divisions of a regular pentagon into triangles and quadrangles

Given n, the number of sides of the polygon, compute the number of such divisions.

The input contains multiple test cases. Each test case consists of a single integer n (3 ≤ n ≤ 5000) on a separate line. The input ends where EOF is met.

For each test case, print the answer modulo 2⁶⁴ on a separate line.

3
4
5
6
7
8
9
10

1
3
10
38
154
654
2871
12925